Random Effects Model
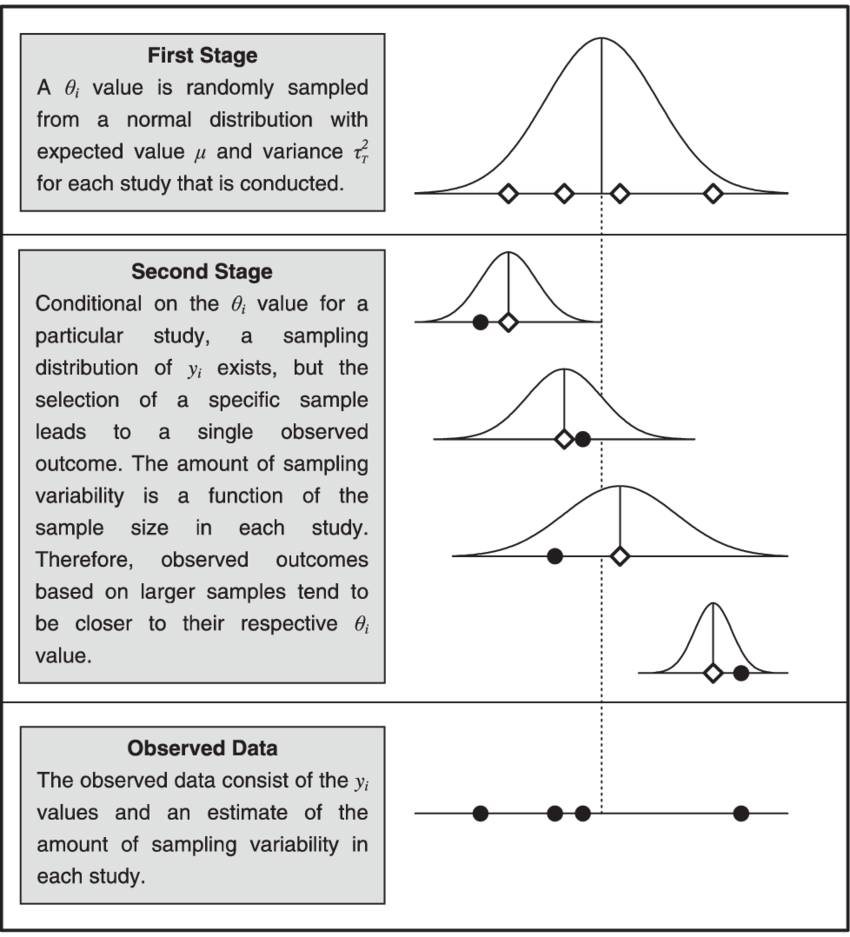
In the realm of statistics, researchers often grapple with the challenge of accounting for variability within data sets, especially when dealing with complex and multifaceted phenomena. The random effects model emerges as a powerful tool to address this challenge, offering a nuanced perspective on the underlying structures governing observed variability. From social sciences to biomedical research, the random effects model finds extensive application, providing insights into diverse fields of study.
Table of Contents
ToggleUnveiling the Essence of Random Effects Model
At its core, the random effects model acknowledges that not all sources of variability in a dataset are explicitly measured or known. It assumes that the observed data are influenced by both fixed effects, which represent systematic influences that are constant across observations, and random effects, which encapsulate unobserved or latent factors contributing to variability. This model distinguishes itself by allowing these random effects to be drawn from a broader population distribution, thus accommodating the inherent diversity and heterogeneity within the data.
Bridging Theory and Application
The utility of the random effects model transcends theoretical abstraction, finding practical application in a myriad of research domains. In longitudinal studies, for instance, where observations are collected over time from the same subjects, random effects capture individual-level variations that persist across multiple measurements. This enables researchers to discern trends and patterns that may otherwise remain obscured by transient fluctuations.
Similarly, in meta-analysis, where data from multiple studies are synthesized to draw overarching conclusions, random effects accommodate variations between studies by acknowledging that effect sizes may differ not only due to sampling error but also due to genuine differences in underlying population parameters. This nuanced approach fosters more robust and generalizable findings, enhancing the reliability and validity of meta-analytic results.
Challenges and Considerations
Despite its versatility and utility, the random effects model is not without its challenges. Estimating the parameters of the model, particularly in the presence of correlated random effects or small sample sizes, can be computationally demanding and prone to bias. Moreover, interpreting the results requires careful consideration of the underlying assumptions, as violations of these assumptions can undermine the validity of conclusions drawn from the model.
Furthermore, determining whether to employ a random effects or fixed effects model necessitates thoughtful deliberation, as each approach entails distinct assumptions and implications for the interpretation of results. While random effects models offer greater flexibility and generalizability by accounting for unobserved heterogeneity, fixed effects models may be more appropriate when focusing on specific groups or contexts with limited interest in generalizability beyond the sampled units.
Future Directions and Innovations
As statistical methodologies continue to evolve in tandem with advancements in computational power and data analytics, the random effects model stands poised to undergo further refinement and innovation. Bayesian approaches, for example, offer a promising avenue for extending the random effects framework by incorporating prior knowledge and uncertainty into the modeling process. Similarly, hierarchical modeling techniques enable the hierarchical structuring of random effects, allowing for more nuanced representations of complex data structures.
Moreover, as interdisciplinary collaboration becomes increasingly prevalent in scientific research, the integration of random effects models with machine learning algorithms and artificial intelligence holds the potential to unlock new insights and discoveries across diverse domains. By harnessing the complementary strengths of statistical modeling and computational techniques, researchers can unravel the intricacies of complex systems with unprecedented depth and granularity.
Conclusion
In the mosaic of statistical methodologies, the random effects model shines as a beacon of sophistication and versatility, offering a nuanced lens through which to analyze and interpret the complexities inherent in empirical data. From longitudinal studies to meta-analytic syntheses, this model empowers researchers to navigate the intricate landscape of variability, illuminating hidden patterns and uncovering deeper insights. As we venture into an era defined by data-driven inquiry and interdisciplinary collaboration, the random effects model remains an indispensable tool for unlocking the mysteries of the universe, one observation at a time.






